Systematically Improving Espresso

The modern coffee market aims to provide products that are both consistent and have desirable flavour characteristics. Espresso fulfils both these requirements making it one of the most widely consumed coffee formats. It is brewed using hot water, forced through a bed of roasted coffee at high pressure. This makes Espresso susceptible to variation in quality. However, the origin of this inconsistency has traditionally and incorrectly been attributed to human variations. A mathematical model, paired with an experiment aiming to reduce variation and the waste produced, has shown positive results and has elucidated that the grinder and water pressure play pivotal roles in achieving beverage reproducibility.

A coffee machine dynamically controls both water pressure and temperature, but other variables impact the beverage quality before the ground coffee is exposed to water. The grind setting determines the particle size distribution of the coffee grounds and, therefore, the surface area. Once compacted into a granular bed, the particle size distribution plays a role in controlling the permeability of the bed and, consequently, the flow rate. A multi-scale mathematical model for extraction from a granular bed is applied to espresso-style coffee extraction. The model offers scope to independently alter familiar variables such as grind setting, water pressure, flow rate, coffee dose and extraction kinetics.

These culminate in a prediction of extraction yield, a ratio of solvated coffee mass to the mass of dry coffee used to produce the beverage, to assess extraction. The model helps understand the origin of irreproducibility in Espresso and then proposes a novel strategy for minimizing drink variation and dry coffee waste. The model ignores the brew time and navigates the EY landscape using only the mass of coffee and water as independent variables.

In this model, Espresso is brewed in a cylindrical container given above. The solid coffee grounds occupy a part of the cylinder and contain a concentration of soluble coffee, Cs. The cylinder also contains inter-granular pore space, Ui, which is occupied by liquid during extraction, which contains a concentration of coffee solubles Cl. An overpressure applied by a pump drives the liquid flow between the inlet (z = 0) and outlet (z = L).

The model takes the form of a system of partial differential equations that describe the transport of coffee solubles from the interior of the grounds to their surface, the exchange or dissolution of the solubles from the grounds into the liquid, and the migration of the solubles in the liquid by a combination of diffusion and advection. A combination of diffusion and convection transports the solubles in the liquid phase due to the flow of the liquid through the bed. The concentration of solvated coffee is therefore governed by an advection-diffusion equation:

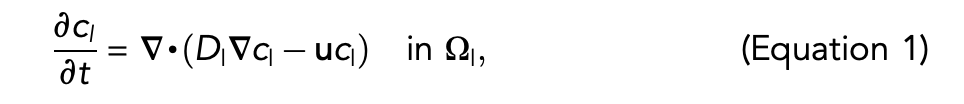
where t, Dl, and u are time, the diffusivity of solubles within the liquid, and the velocity of the liquid, respectively. The liquid flow is solved via the Navier-Stokes equations:

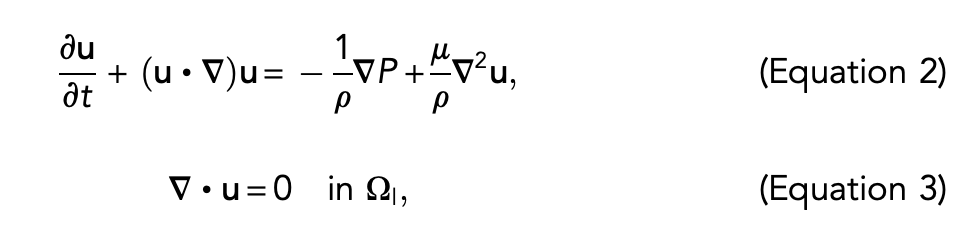
where μ, p and P are liquid viscosity, density and overpressure respectively.

Work by Spiro and colleagues demonstrated that the transport of coffee solubles through the interior of the grounds can be described by a diffusion process. Hence,

where Ds is the diffusivity of solubles within the grains.

Boundary conditions at the inlet, z = 0, include a specified fluid overpressure, the requirement that the water enters the basket with a purely normal velocity, and that the normal flux of dissolved species should be zero:

where t^ and n^ are the unit vectors tangent and normal to the surface z = 0, respectively. At the exit, we apply conditions of zero overpressure, zero tangential velocity, and a condition that there is zero diffusive flux of coffee. In summary,

At the vertical edges of the cylinder, R = R0, no flux conditions are applied to the liquid coffee concentration, because the liquid cannot exit in these directions:

On the boundaries between the grains and inter-granular pore space, R int, there is a

flux of solubles per unit area, which we denote by G. Appropriate boundary condi-

tions are

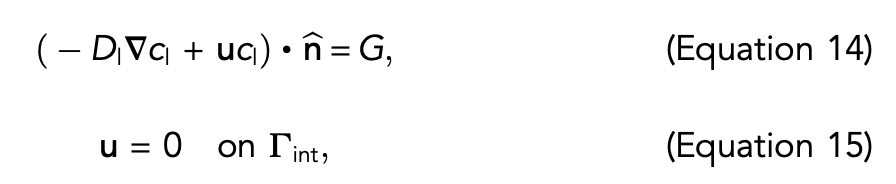
where the former two capture mass transfer and the latter imposes that the liquid should be stationary on the grain/pore space interface.

Determining the form of the reaction rate, G, is non-trivial. However, it can be reasonably assumed that the rate of transfer of solubles between the phases should depend on the local concentrations of solubles near the interface. Furthermore, the rate of extraction is zero when the liquid immediately outside the grain is saturated or when the grain is depleted of solubles. Therefore a rate is assumed that satisfies all of the above conditions, namely where k is a rate constant.

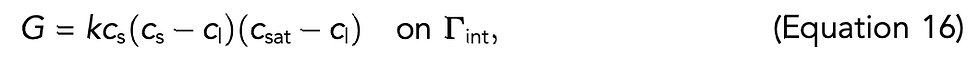
Coffee particulates remain dry until they are connected to the extraction apparatus, at which point water is rapidly introduced to the bed, serving to wet the entire puck and stabilize the particle temperature. Modelling this initial wetting stage poses another series of interesting problems. Modelling of this stage is avoided by assuming that at t = 0 when extraction begins, the bed is filled with liquid water that is free from solubles. We therefore have

The model predicts that EY can be increased by grinding less and finer coffee using lower pressure water. The model can faithfully reproduce experimental measurements in regimes where flow is homogeneous and accurately predicts EYs as a function of meaningful parameters, such as coffee mass, water mass, and extraction rates. While the EY is not directly indicative of quality, it does allow for economic arguments to be made. If the model is widely implemented, this protocol will have a significant economic impact and create a more sustainable coffee-consuming future.