Euler’s disk

Euler’s Disk, invented between 1987 and 1990 by Joseph Bendik, is a trademark for a scientific-educational toy. It is used to illustrate and study the dynamic system of spinning and rolling disks on a flat or curved surface. The Euler’s Disk is known for the uncanny way its spin rate speeds up as the disk loses energy. It takes a mind-boggling amount of time for the disk to stop spinning. As the disk rolls on the base, the latter is deformed. If we roll the same disk on a smooth, hard surface such as a granite surface plate, the motion dies out more, and rattling sounds are more prominent. A slight amount of flexibility in the base is important in damping the perturbations of the rolling motion if long spin times are to be achieved.

When Euler’s Disk is spun, it contains both potential and kinetic energy. The potential energy is given to the disk when it is placed upright on its side. The kinetic energy is given to the disk when it is spun on the mirrored base. Euler’s disk would continue to spoil (spin and roll) forever if friction and vibration did not exist. Euler’s disk behaves this way because of its angular momentum. Like a top, Euler’s Disk uses its angular momentum to hold itself upright. As the disk spoils around in a circle it is held in place by a balance of the gravitational force pulling the disk down and the force applied by the mirror base which holds the disk up. Using Euler’s equations of motion - and several assumptions - one can show that as the disk loses energy, the soaring pitch produced by the rolling point of contact increases towards infinity, as the inverse square root of the angle alpha. The disk ultimately comes to rest. The last stage of motion is accompanied by a whirring sound of increasing frequency. It also loses gravitational potential energy by an equal amount. This means that the centre-of-mass of the disk must drop in height, which causes the angle of the disk to get smaller and smaller. This causes the disk to spoil faster and faster.

Now to analyze the physics of Euler's disk let us start off by drawing a schematic (shown below) which illustrates the disk spoiling on a flat surface.

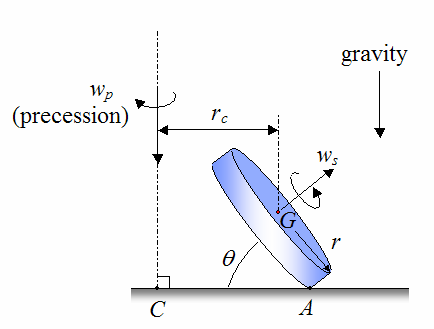
Where:

ws is the rate of spin of the disk, in radians/second

wp is the rate of precession, in radians/second

A is the contact point between the disk and the flat surface

C is the point where the axis of precession intersects the flat surface

rc is the horizontal distance from the axis of precession to the center of mass G of the disk, as shown. It is assumed that the center of mass of the disk coincides with the geometric center of the disk.

r is the radius of the disk

θ is the angle between the horizontal and the disk

We treat ws, wp, and θ as constant. To simplify the understanding of the motion of the disk we need to make some assumptions which include:

-The disk rolls on the flat surface without slipping

- The disk is thin relative to its radius

- The disk rolls such that rc = 0. This is approximately true as θ becomes small.

With simplifying assumptions in mind, let's now redraw the schematic. The disk is treated as "thin" such that the thickness can be neglected.

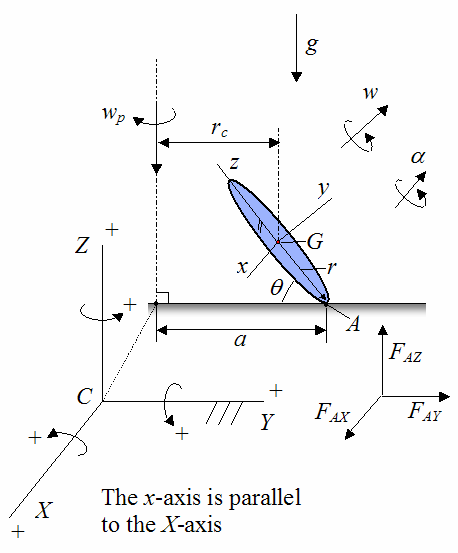
Where:

A global XYZ axes is defined as shown, with origin at point C, and fixed to ground

A local xyz axes is defined as shown, with origin at point G, and attached to the disk so that it moves with the disk. Note that this axes is aligned with the principal directions of inertia of the disk. Also note that the local x-axis is parallel to the global X-axis

g is the acceleration due to gravity

w is the angular velocity of the disk, with respect to ground

α is the angular acceleration of the disk, with respect to ground

a is the distance from point C to point A

FAX is the force acting on the disk in the global X-direction, at point A

FAY is the force acting on the disk in the global Y-direction, at point A

FAZ is the force acting on the disk in the global Z-direction, at point A

Lastly, we shall define I, J, and K as unit vectors pointing along the positive directions of the global X, Y, and Z axis respectively

The angular velocity of the disk, with respect to ground, is

The angular acceleration of the disk, with respect to ground, is

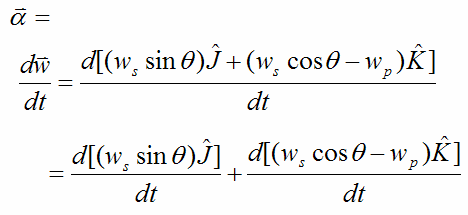
Looking at the first term:

Looking at the second term:

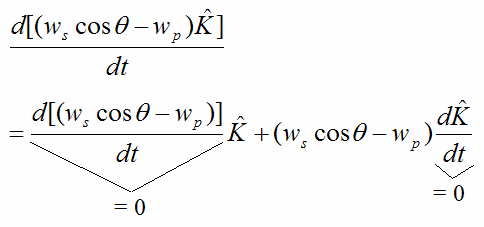
Therefore, for the disk

The Euler’s disk is a fascinating toy that not only entertains us but also helps us to understand Math and the physics behind it which enhances our skills.