The Heat equation and the Fourier Series

Most of us have learned and implemented equations related to thermal effects in our lives and have come across various terms like latent heat or specific heat capacity which is one of the basic concepts in Physics. By using many of these basic concepts we will be explaining the heat equation and its significance in Maths and our lives.

A partial differential equation is an equation that relates a function with more than one variable to its partial derivatives and one of the most prominent partial differential equations is the heat equation that describes the distribution of heat or the temperature field in a given body over time. Given below is the heat equation:

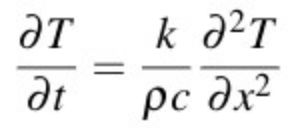
In this equation, the temperature T is a function of position x and time t, and k, ρ, and c are, respectively, the thermal conductivity, density, and specific heat capacity of the metal, and k/ρc is called the diffusivity.

The temperature distribution in any body depends on three things: The initial temperature distribution T(x,0) known as the initial condition, the temperature at the ends of the bar, T(0,t) and T(L,t) and finally a law governing the rules for the transfer of heat from one point to another within a body. The heat equation is a mathematical representation of such a physical law.

The heat equation can be derived from the law of conservation of energy: the time rate of change of the heat stored at a point on the bar is equal to the net flow of heat into that point. This process clearly obeys the continuity equation. If Q is the heat at each point and V is the vector field giving the flow of the heat, then:

According to the Second Law of Thermodynamics, if two identical bodies are brought into thermal contact and one is hotter than the other, then heat must flow from the hotter body to the colder one at a rate proportional to the temperature difference. Therefore V is proportional to the negative gradient of the temperature, so V=-k∇T where k is the thermal conductivity of the metal. In one dimension this reduces to V=(-k∂T/∂x)x where x is the unit vector in the +x-direction. Furthermore, Q=ρcT, so we get the heat equation by plugging in these expressions for V and Q:

It can be extremely hard to solve this equation without using the Fourier series which plays a vital role.

Fourier series is an expansion of a periodic function ‘f(x)’ in terms of an infinite sum of sines and cosines. Fourier series make use of the orthogonality relationships of sine and cosine function.The computation and study of Fourier series is known as harmonic analysis and is extremely useful as a way to break up an arbitrary periodic function into a set of simple terms that can be plugged in, solved individually, and then recombined to obtain the solution to the original problem or an approximation to it to whatever accuracy is desired or practical.

The mathematical formula of the fourier series is given below:

Now we can relate this equation to the explanation given before. So in order to compute the Fourier series representation of some periodic function f, therefore, one needs only to compute the above set of integrals for arbitrary k.

The series was originally devised as a method of solving the heat equation.

The laws of thermodynamics tell us that no matter what the temperature distribution of a body is initially, the system must undergo a process that brings the body to thermal equilibrium, so solutions to the heat equation exist for physically meaningful initial and bound conditions.

This means that if f(x,t) and g(x,t) are two different functions that satisfy the same IBVP for the heat equation, then f and g have the same form. Also the heat equation is linear so if f and g are solutions and α and β are any real numbers, then αf+βg is also a solution. So we can conclude that the solution is going to be a linear combination of functions of the same form.

Consider the following function:

Where n is a positive integer, this function satisfies the heat equation:

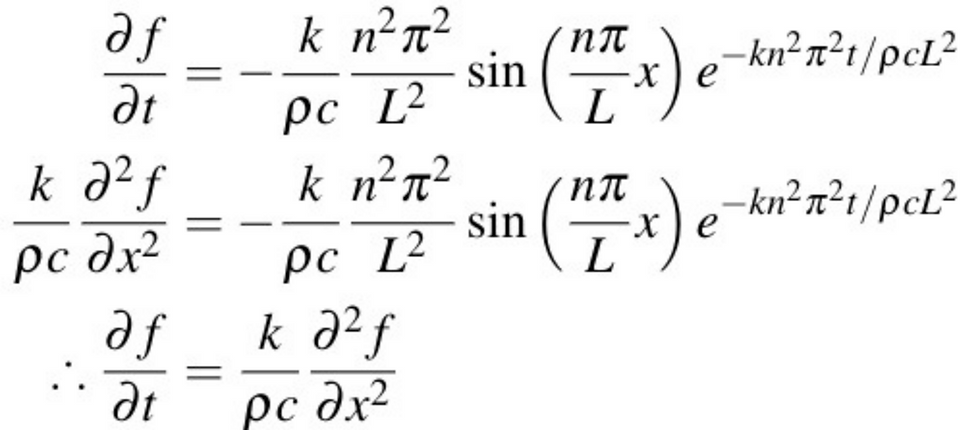
This function also satisfies the boundary conditions since sin(0)=sin(nπ)=0. Therefore the general solution is:

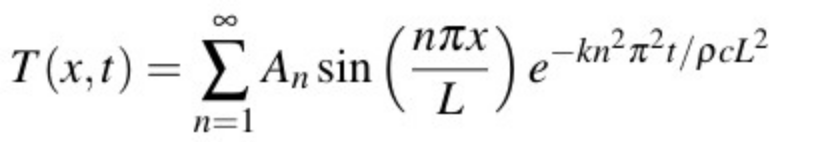
The problem will be solved if we can find the coefficients (An) such that this general solution satisfies the initial condition. That is, we need to find (An) such that:

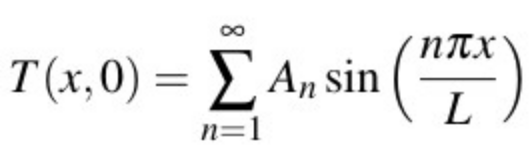
This is called a Fourier sine series expansion for the initial conditions. The coefficients ( An) in this equation are Fourier coefficients, This is where the Fourier series plays a role in solving the Heat equation. The way of finding the Fourier coefficients given above can be used in this equation.

This shows how the heat equation is so closely connected to the Fourier series. There are many other uses of Fourier series which make it extremely important in mathematics. The heat equation also helps us to understand the properties of a material which helps us use it efficiently.